1. NOTION DE PARAMETRE.

1. Ecriture d'un algorithme paramétrique.

Nous avons vu qu'un algorithme est constitué par une séquence d'actions, les unes étant des actions élémentaires ou primitives, les autres étant des actions composées, c'est à dire des algorithmes déjà connus.

Pour pouvoir utiliser ces algorithmes dans des environnements différents, nous allons devoir placer des variables en paramètres.

Considérons le problème suivant :

Un article est vendu 12,5 Frs l'unité, si la quantité demandée est inférieure à 100. Il est vendu 40 % moins cher ,si la quantité demandée est supérieure à 100 unités.

On souhaite écrire un programme qui calcul le montant global de la facture en fonction de la quantité achetée, saisie au clavier.

Ecriture de l'algorithme.

Déclarations des variables et des constantes.

VARIABLE	TYPE	SIGNIFICATION
Qté Prix_ven Total_fac	Entier Réel Réel	Quantité d'articles achetés Prix de vente de l'article en fonction de la quantité achetée Montant de la facture

 

CONSTANTES	TYPE	VALEUR	SIGNIFICATION
Pu	Réel	12,5	Prix unitaire de référence

Définition des paramètres.

DONNEES RESULTATS

Instructions

ALGORITHME FACTURE ()

DEBUT

ECRIRE ("Quantité achetée?")

LIRE(Qté)

SI Qté = 100

ALORS

Prix_ven Pu * 0,6

SINON

Prix_ven Pu

FINSI

Total_fac Prix_ven * Qté

FIN

Supposons que, dans le cadre de résolution de problèmes plus importants plusieurs personnes aient besoin de faire appel à ce calcul de prix.

Pour simplifier ces opérations et afin de ne pas avoir dans chacun des programmes à réécrire l'algorithme, nous allons paramètrer l'algorithme afin de lui permettre de travailler directement sur les variables utilisées par les différents utilisateurs.

Pour ce faire, nous allons modifier l'algorithme de la manière suivante :

Déclarations des variables et des constantes.

VARIABLE	TYPE	SIGNIFICATION
Prix_ven Qté Total_fac	Réel Entier Réel	Prix de vente de l'article en fonction de la quantité achetée Nombre d'articles achetés Montant de la facture

CONSTANTES	TYPE	VALEUR	SIGNIFICATION
Pu	Réel	12,5	Prix unitaire de référence

Définition des paramètres.

DONNEES Qté RESULTATS Total_fac

Instructions

ALGORITHME FACTURE (Qté , Total_fac)

DEBUT

SI Qté = 100

ALORS

Prix_ven Pu * 0,6

SINON

Prix_ven Pu

FINSI

Total_fac Prix_ven * Qté

FIN

2. Intérêt des paramètres :

L'intérêt d'utiliser des paramètres, est que l'algorithme se comporte maintenant comme une primitive. Il est ainsi capable de s'exécuter en faisant jouer
à d'autres variables les rôles de Qté et Total_fac. Il va pouvoir
ainsi être utilisé sans modification dans des environnements différents.

3. Paramètres formels et paramètres effectifs :

Un appel d'algorithme consiste à écrire le nom de l'algorithme,
suivi s'il y a lieu d'une liste de paramètres.

Un paramètre formel est une variable choisie comme paramètre à la définition d'un algorithme (il est là pour 'la forme', pour définir l'emplacement).

Un paramètre effectif est une variable utilisée dans un appel
à la place d'un paramètre formel.

A l'exécution d'un appel, la correspondance entre un paramètre formel et un paramètre effectif est définie par leur position dans la liste.

Le premier paramètre effectif correspond au premier paramètre formel, le deuxième paramètre effectif correspond au deuxième paramètre formel, et ainsi de suite.

La notion de paramètres formels et de paramètres effectifs est identique à celle que l'on rencontre en mathématiques dans la notion de fonction. Ainsi si l'on définit f(x,y) = xy, on peut construire une procédure calcul(x,y,z) dont l'unique instruction sera z x * y. Les paramètres formels sont x, y et z..

Si l'on veut calculer la valeur de cette fonction au point particulier (2,3) et affecter le résultat obtenu à la variable U, on appelle :

Calcul(2,3,U)

2, 3 et U sont les paramètres effectifs de l'appel.

Le résultat de cet appel affecte à U la valeur 6.

Ainsi, on distingue deux catégories de paramètres :

4. Les paramètres données :

Le paramètre d'un module est un paramètre- donnée lorsque sa valeur initiale
est utilisée par le module et reste inchangée après l'exécution de ce dernier.

5. Les paramètres résultats :

Le paramètre- résultat (ou donnée -résultat) est un paramètre dont la valeur peut être remplacée en fin d'exécution par une valeur différente de la valeur initiale.

Dans l'exemple de la procédure calcul(x,y,z).

x et y sont des paramètres-données

z un paramètre-résultat

6. Passage par valeur, passage par adresse :

1. Passage par valeur :

Lecture seulement (paramètres- données) : Passage par valeur

Le module agit sur la copie locale, mais pas sur l'original.

Dans un passage par valeur, c'est la valeur du paramètre et
non son nom qui est transmis au sous-programme.

2. Passage par adresse :

Lecture/écriture (paramètres- résultats) : Passage par Adresse ou par Variables .

Dans ce cas, le module connaît l'adresse en mémoire du paramètre effectif, et travaille directement à cette adresse sur l'original.

Un paramètre résultat ne peut jamais être transmis par valeur.

EXEMPLE: Soit un algorithme qui effectue la somme de deux nombres passés en paramètre et qui restitue le résultat dans un troisième paramètre.

Déclarations des variables et des constantes.

VARIABLE	TYPE	SIGNIFICATION
X Y Z	Réel Réel Réel	Première valeur à additionner Deuxième valeur à additionner Résultat de l'opération

Définition des paramètres.

DONNEES X , Y RESULTATS Z

Instructions

ALGORITHME SOMME (X,Y,Z)

DEBUT

Z X+ Y

FIN

APPEL DU SOUS-PGM AU SEIN D'UN AUTRE PROGRAMME:

a 2

b 3

SOMME(a,b,c)

A l'appel du sous-programme il y a substitution entre les paramètres formels et les paramètres effectifs.

Le passage des paramètres se fait par valeur ou par adresse en fonction de ce qui a été décidé dans la déclaration des paramètres de l'algorithme appelé.



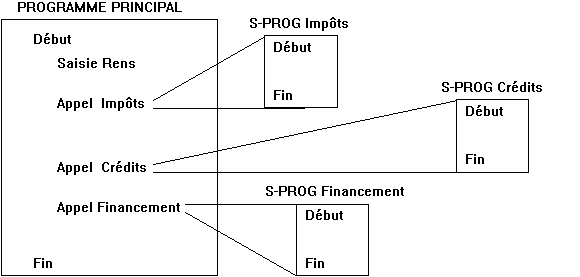
3. Variables globales et variables locales :

Les variables globales, déclarées dans la partie Déclaration de l'algorithme principal, sont accessibles depuis n'importe quel point du programme, aussi bien du sous-programme que du programme principal.

Les variables locales, déclarées dans les parties Déclaration des différents sous-programmes, ne sont accessibles que par celles-ci, c'est à dire qu'elles ne peuvent être utilisées que dans les instructions du sous-programme où elles sont déclarées.

2. NOTION DE FONCTION ET DE PROCEDURE :

1. Intérêts :

Ces deux nouveaux modules, très importants, permettent au programmeur de traiter un problème sans s'embarrasser, dans un premier temps, du règlement dans le détail des sous- problèmes le composant.

L'utilisation des fonctions et procédures offre un autre intérêt évident dans la résolution d'un problème où l'on est amené à résoudre plusieurs fois le même sous- problème. On utilise alors un algorithme de ce type pour éviter d'écrire plusieurs fois la même suite d'instructions.

Il faut ajouter enfin la plus grande facilité de mise au point et de maintenance des programmes, voire la possibilité de faire écrire par plusieurs personnes les différentes parties d'un algorithme.

2. Caractéristiques :

Une fonction ou une procédure est un bloc d'instructions,
nommé et paramétré que l'on déclare afin de pouvoir ensuite l'appeler
par son nom en affectant des valeurs aux paramètres.

Le résultat d'une fonction ou d'une procédure est évalué chaque fois que l'on l'appelle.

3. Différences entre fonction et procédure :

La procédure retourne le résultat par l'intermédiaire du paramètre ‘’résultat’. Dans le cas de la fonction le résultat est désigné par le nom même de la fonction.

1. Les particularités des fonctions :

Elles sont assez proches de la notion mathématique correspondante.

Une fonction possède des arguments qui correspondent aux informations qui lui sont transmises afin qu'elle fournisse un résultat principal (unique et simple). Ce résultat est désigné par le nom même de la fonction.

L'appel d'une fonction peut avoir lieu au sein d'une expression.

2. Les particularités des procédures :

Elles peuvent, posséder des paramètres mais ce n'est pas obligatoire.

Elles n'ont pas de valeurs propres. Lorsqu'elles sont destinées à restituer des résultats elles le font par l'intermédiaire de paramètres résultat.

L'appel d'une procédure ne peut avoir lieu au sein d'une expression.

4. Parallèle entre procédure et fonction :

Toute procédure qui ne comporte qu'un paramètre résultat
peut être remplacée par une fonction.

Les fonctions sont des procédures particulières qui possèdent résultat

principal "constitué" par le nom de la fonction lui-même.

5. les prédicats :

Les prédicats sont des fonctions particulières ne délivrant qu'un résultat principal booléen (VRAI ou FAUX)

Home