1. Formalisme de l’alternative ‘’SOIT SOIT’’ en algorithmique :

- Les termes relatifs aux structures sont écrits en majuscules et soulignés.

- Le début de structure est relié à la fin de structure par un trait vertical.

- Les structures alternatives de ce type commencent par SI condition(s) puis ALORS (et selon le cas) SINON et se terminent par FIN SI.

SI condition

ALORS

Instruction 1

Instruction 2

SINON

Instruction 3

FIN SI

2. Principe :

Reprenons l’exemple du café :

1) Mettre l’eau dans la cafetière

2) Mettre un filtre

3) Mettre le café dans le filtre

4) Appuyer sur le bouton de mise en route

Nous pouvons considérer que notre description manque de précision : comment se présente le café, en grains ou moulu ? Les actions sont différentes dans les deux cas.

SI café en grains

Nous répétons dans les deux cas la même action, (mettre le café moulu dans le filtre), nous pouvons donc simplifier l’écriture de l’analyse de la manière suivante.

SI café en grains

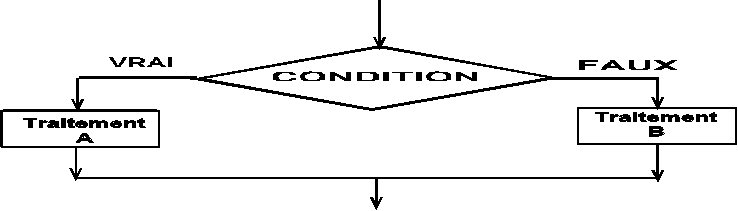
SI la condition est vraie, le traitement A sera effectué, SINON c’est le traitement B qui le sera et la dernière action, (mettre le café) sera systématiquement exécutée.

Soit l’ensemble des lettres de l’alphabet. La proposition ‘’est une voyelle’’ est un PREDICAT.

- LES PREDICATS ELEMENTAIRES :

Ce sont les opérations élémentaires à résultat booléen.

Lorsque l’utilisation de comparaison ne suffit pas à exprimer une situation, on utilise les prédicats composés qui sont des expressions d’objets de type booléen.

2. Choix Multiple :

1. Formalisme de la structure conditionnelle ‘’AU CAS OU’’ :

- Les termes relatifs aux structures sont écrits en majuscules et soulignés.

- Le début de structure est relié à la fin de structure par un trait vertical.

- Les structures alternatives de ce type commencent par AU CAS OU nom de la variable, suivie de chacune des valeurs que peut prendre cette variable avec leurs instructions correspondantes et se terminent par FIN CAS.

AU CAS OU VAR =

VAL1 : Instruction1

VAL2 : Instruction2

VALN : Instruction N

FIN AU CAS OU

2. Principe :

Notre café ne peut avoir initialement que deux états. Lorsque la condition testée ne peut prendre qu’un nombre relativement faible de valeurs bien définies, on peut utiliser une autre structure d’alternative appelée AU CAS OU.

2. REPETITION CONDITIONNELLE D’ UNE ACTION (ITERATIONS)

1. Généralités :

On appelle ITERATION toute répétition de l’exécution d’une action.

 

Il apparaît nécessaire de disposer de structures algorithmiques permettant de décrire de façon commode une itération, que l’on connaisse ou non le nombre de répétitions.

2. Itération avec début de boucle  :

1. Formalisme de la structure itérative ‘’TANT QUE’’

Les structures itératives avec test en début de boucle commencent par

TANT QUE condition(s) puis FAIRE et se terminent par FIN FAIRE.

 

TANT QUE condition ou booléen

FAIRE

Instruction1

Instruction2

FIN FAIRE

2. Principe :

Reprenons l’exemple du café.

Considérons maintenant que l’on veuille adapter la qualité de café mise dans le filtre en fonction de la quantité de tasses à produire.

L’action METTRE DU CAFE peut se décompose en :

Remplir une mesure

Verser la mesure dans le filtre

Cependant si une seule mesure n’est pas suffisante, nous devons reproduire plusieurs fois ces deux mêmes actions.

L’analyse devient alors :

TANT QUE le café est insuffisant

L’expression qui suit le TANT QUE exprime la condition à respecter pour que l’action se répète.

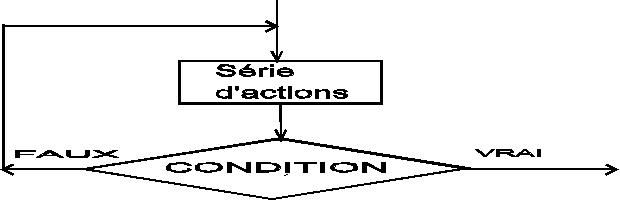
On constate que le test est effectué avant de faire, ne serait ce qu’une fois, les actions concernées par la boucle.

Si la condition est fausse d’entrée, il n’y a pas exécution de la boucle. Les actions qui font partie de la boucle peuvent donc être exécutées un nombre de fois variant de

0 à N.

Ce type de structure est appelé :

1. Formalisme de la structure itérative ‘’REPETER JUSQU’A’’ :

Les structures itératives avec test en fin de boucle commencent par :

REPETER se terminent par JUSQU’A condition ou booléen.

REPETER

Instruction1

Instruction2

Instruction3

JUSQU’ A condition ou booléen

2. Principe :

L’itération avec test de fin de boucle permet d’être sûr de faire au moins une fois le traitement qui se trouve dans le corps de la boucle.

3. REPETITION SANS CONDITION D’UNE ACTION

1. Formalisme de la structure itérative ‘’POUR I variant ...’’

Les termes relatifs aux structures sont écrits en majuscules et soulignés.

Le début de structure est relié à la fin de structure par un trait vertical.

Les structures itératives comprenant un nombre précis d’itérations commencent par POUR var VARIANT de ‘’I’’ à ‘’J’’ (au pas de ‘’K’’)

puis FAIRE et se terminent par FIN FAIRE.

POUR var VARIANT de ‘’I’’ à ‘’J’’ (au pas de ‘’K’’)

FAIRE

Instruction1

Instruction2

Instruction3

FIN FAIRE

Si le pas n’est pas précisé, il est implicitement égal à 1. Le pas d’ incrémenta-

tion peut être négatif (dans ce cas-là les bornes doivent être bien sûr être inversées).

Attention au langage utilisé.

2. Principe :

Reprenons l’exemple du café.

Considérons maintenant que l’on veuille adapter la qualité de café mise dans le filtre en fonction du nombre de tasses à produire et que ce nombre soit égal à 10.

Si l’on considère qu’à une mesure correspond une tasse.

Les actions ‘’Remplir une mesure’’ et ‘’verser la mesure dans le filtre’’ vont être à exécuter 10 fois.

le principe revient donc à compter le nombre de fois que l’on fait l’action, et à s’arrêter lorsque ce nombre est égal à 10.

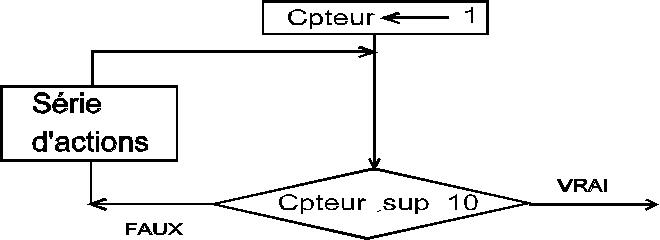
Pour faciliter la compréhension, on peut considérer que l’on a un compteur qui s’incrémente à chaque fois que l’on fait la série d’actions concernées et que l’on teste régulièrement pour savoir si l’on est arrivé à 10.

L’analyse devient alors :

TANT QUE je ne l’ai pas fait 10 fois

Ce type de structure peut se représenter schématiquement de la manière suivante :

Home